☰
Navigation :

word2vec

在信号处理领域，图像和音频信号的输入往往是表示成高维度、密集的向量形式，在图像和音频的应用系统中，如何对输入信息进行编码(Encoding)显得非常重要和关键，这将直接决定了系统的质量。然而，在自然语言处理领域中，传统的做法是将词表示成离散的符号，例如将 [cat] 表示为 [Id537]，而 [dog] 表示为 [Id143]。这样做的缺点在于，没有提供足够的信息来体现词语之间的某种关联，例如尽管cat和dog不是同一个词，但是却应该有着某种的联系（如都是属于动物种类）。由于这种一元表示法(One-hot Representation)使得词向量过于稀疏，所以往往需要大量的语料数据才能训练出一个令人满意的模型。而Word Embedding技术则可以解决上述传统方法带来的问题。

向量空间模型(Vector space models, VSMs)将词语表示为一个连续的词向量，并且语义接近的词语对应的词向量在空间上也是接近的。VSMs在NLP中拥有很长的历史，但是所有的方法在某种程度上都是基于一种分布式假说，该假说的思想是如果两个词的上下文(context)相同，那么这两个词所表达的语义也是一样的；换言之，两个词的语义是否相同或相似，取决于两个词的上下文内容，上下文相同表示两个词是可以等价替换的。

基于分布式假说理论的词向量生成方法主要分两大类：计数法(count-based methods, e.g. Latent Semantic Analysis)和预测法(predictive methods, e.g. neural probabilistic language models)。Baroni等人详细论述了这两种方法的区别，简而言之，计数法是在大型语料中统计词语及邻近的词的共现频率，然后将之为每个词都映射为一个稠密的向量表示；预测法是直接利用词语的邻近词信息来得到预测词的词向量（词向量通常作为模型的训练参数）。

Wrod2vec是一个典型的预测模型，用于高效地学习Word Embedding。实现的模型有两种：连续词袋模型(CBOW)和Skip-Gram模型。算法上这两个模型是相似的，只不过CBOW是从输入的上下文信息来预测目标词(例如利用 [the cat sits on the] 来预测 [mat] )；而skip-gram模型则是相反的，从目标词来预测上下文信息。一般而言，这种方式上的区别使得CBOW模型更适合应用在小规模的数据集上，能够对很多的分布式信息进行平滑处理；而Skip-Gram模型则比较适合用于大规模的数据集上。

Skip-Gram模型

基于神经网络的概率语言模型通常都是使用最大似然估计的方法进行训练的，通过Softmax函数得到在前面出现的词语 $$h$$ (history)的情况下，目标词 $$w_t$$ (target)出现的最大概率，数学表达式如下：

$$ P(w_t | h) = {softmax}(\text{score}(w_t, h)) = \frac{\exp { \text{score}(w_t, h) } }{\sum_\text{Word w’ in Vocab} \exp { \text{score}(w’, h) } }$$

其中，$$score(w_t,h)$$为词 $$w_t$$ 和上下文$$h$$的兼容程度。上式的对数形式如下：

$$ J_\text{ML} = \log P(w_t | h) = \text{score}(w_t, h) -\log \left( \sum_\text{Word w’ in Vocab} \exp { \text{score}(w’, h) } \right)$$

理论上可以根据这个来建立一个合理的模型，但是现实中目标函数的计算代价非常昂贵，这是因为在训练过程中的每一步，我们都需要计算词库 $$w’$$ 中其他词在当前的上下文环境下出现的概率值，这导致计算量十分巨大。

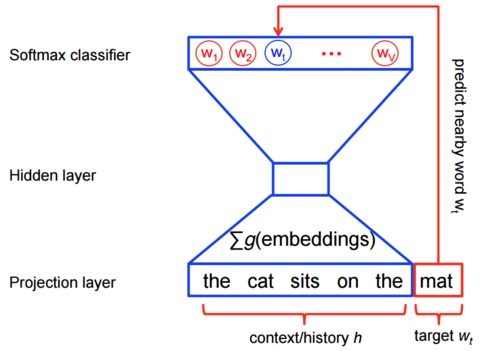
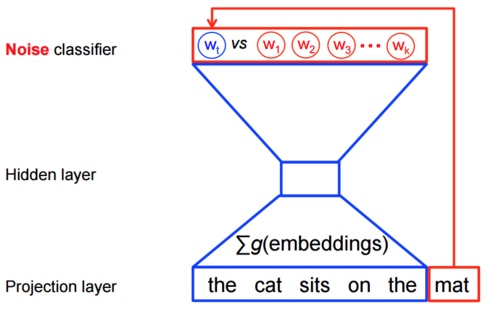
然而，对于word2vec中的特征学习，可以不需要一个完整的概率模型。CBOW和Skip-Gram模型在输出端使用的是一个二分类器(即Logistic Regression)，来区分目标词和词库中其他的 $$k$$ 个词。下面是一个CBOW模型的图示，对于Skip-Gram模型输入输出是倒置的。

此时，最大化的目标函数如下：

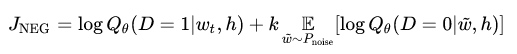
目标函数的意义是显然的，即尽可能的分配高概率给真实的目标词，而低概率给其他 $$k$$ 个 [噪声词]，这种技术称为负采样(Negative Sampling)。同时，该目标函数具有很好的数学意义：即在条件限制(训练时间)的情况下尽可能的逼近原有的Softmax函数（选择 $$k$$ 个 [噪声点] 作为整个 [噪声数据] 的代表），这样做无疑能够大大提升模型训练的速度。实际中我们使用的是类似的噪声对比估计损失函数(noise-contrastive estimation (NCE))，在TensorFlow中对应的实现函数为tf.nn.nce_loss()。

参考文档