数据集拆分
在机器学习中,通常将所有的数据划分为三份:训练数据集、验证数据集和测试数据集。它们的功能分别为
- 训练数据集(train dataset):用来构建机器学习模型
- 验证数据集(validation dataset):辅助构建模型,用于在构建过程中评估模型,为模型提供无偏估计,进而调整模型超参数
- 测试数据集(test dataset):用来评估训练好的最终模型的性能
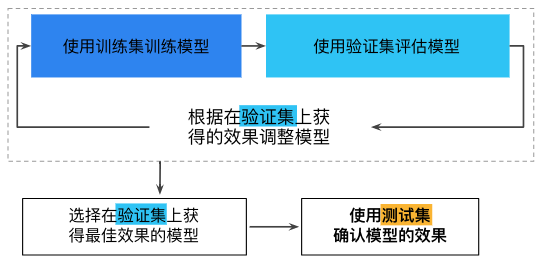
不断使用测试集和验证集会使其逐渐失去效果。也就是说使用相同数据来决定超参数设置或其他模型改进的次数越多,对于这些结果能够真正泛化到未见过的新数据的信心就越低。请注意,验证集的失效速度通常比测试集缓慢。如果可能的话,建议收集更多数据来“刷新”测试集和验证集。重新开始是一种很好的重置方式。
为了划分这几种数据集,可以选择采用留出法、K-折交叉验证法或者自助法等多种方法。这些方法都对数据集有一些基本的假设,包括
- 数据集是随机抽取且独立同分布的
- 分布是平稳的,不会随时间发生变化
- 始终从同一个分布中抽取样本
陷阱:请勿对测试数据集进行训练。
留出法
留出法(hold-out)直接将数据集划分为互斥的集合,如通常选择 70% 数据作为训练集,30% 作为测试集。
需要注意的是保持划分后集合数据分布的一致性,避免划分过程中引入额外的偏差而对最终结果产生影响。通常来说,单次使用留出法得到的结果往往不够稳定可靠,一般采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。
K-折交叉验证法
Kuhn 和 Johnson 在「Data Splitting Recommendations」中指出使用单独的「测试集」(或验证集)具有一定的局限性,包括
- 测试集是对模型的单次评估,无法完全展现评估结果的不确定性。
- 将大的测试集划分成测试集和验证集会增加模型性能评估的偏差。
- 分割的测试集样本规模太小。
- 模型可能需要每一个可能存在的数据点来确定模型值。
- 不同测试集生成的结果不同,这造成测试集具备极大的不确定性。
- 重采样方法可对模型在未来样本上的性能进行更合理的预测。
所以在实际应用中,可以选择 K-折交叉验证(k-fold cross-validation)的方式来评估模型,其偏差低、性能评估变化小。
K-折交叉验证法将数据集划分为 k 个大小相似的互斥子集,并且尽量保证每个子集数据分布的一致性。这样,就可以获取 k 组训练 - 测试集,从而进行 k 次训练和测试。
k 通常取值 10,此时称为 10 折交叉验证。其他常用的 k 值还有 5、20 等。
自助法
自助法(bootstrap method)以自助采样法为基础:每次随机的从初始数据 $D$ 中选择一个样本拷贝到结果数据集 $D’$ 中,样本再放回初始数据 $D$ 中;这样重复 $m$ 次,就得到了含有 $m$ 个样本的数据集 $D’$。这样就可以把 $D’$ 作为训练集,而 D\D'作为测试集。这样,样本在 m 次采样中始终不被采集到的概率为
$$\lim_{m\to\infty} (1-\frac{1}{m})^{m} = 1/e = 0.368$$
自助法的性能评估变化小,在数据集小、难以有效划分数据集时很有用。另外,自助法也可以从初始数据中产生多个不同的训练集,对集成学习等方法有好处。
然而,自助法产生的数据集改变了初始数据的分布,会引入估计偏差。因而,数据量足够时,建议使用留出法和交叉验证法。