支持向量机
支持向量机(Support Vector Machine,SVM它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,学习策略是间隔最大化,最终可转化为一个凸二次规划问题的求解。
直观来看,位于两类训练样本“正中间”的划分超平面效果最好,即中间最粗的那条。
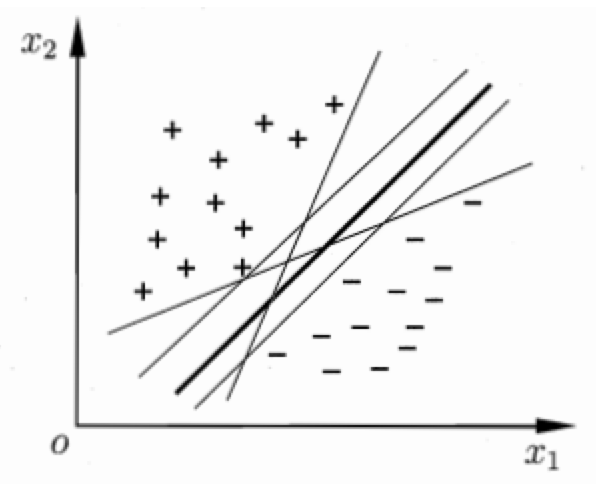
一般使用支持向量机时还会使用核函数,这样支持向量机会成为实质上的非线性分类器。
基本概念
在样本空间中,划分超平面可以定义为线性方程 $$w^Tx+b=0$$。
那么,对应的决策函数为 $$f(x) = sign(w^Tx+b)$$。其中,$$w$$为法向量,决定了超平面的方向;b为位移项,决定了超平面与原点之间的距离。样本空间中任意点x到超平面 $$(w,b)$$ 的距离可写为:
$$r=\frac {w^Tx+b}{||w||}$$
当超平面能将训练样本正确分类时,
$$\left{\begin{matrix} w^Tx_i+b>= +1, y_i=+1\ w^Tx_i+b<= -1, y_i = -1 \end{matrix}\right.$$
如下图,距离超平面最近的这几个训练样本点使上式等号成立,它们被称为“支持向量”(support vector)。
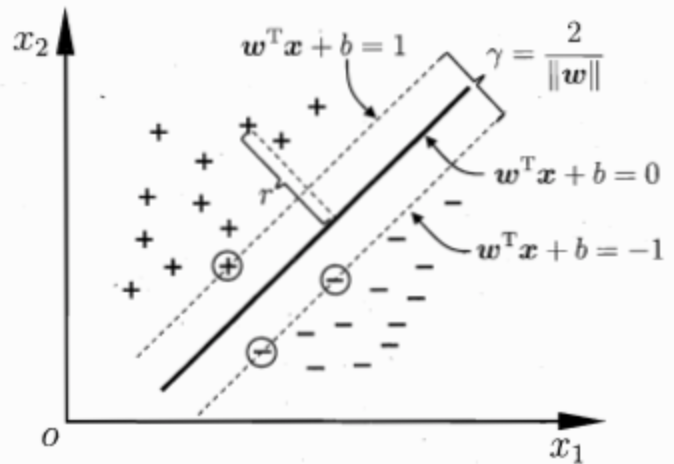
两个异类支持向量到超平面的距离之和称为“间隔”(margin),公式为:$$\gamma = \frac {2} {||w||}$$。
搜寻最大间隔的划分超平面等价于最小化$$||w||^2$$,即
$$\min_{w,b} \frac{1}{2} ||w||^2, s.t. y_i(w^Tx_i+b)>=1$$
这就是支持向量机的基本型。
对偶问题
求解式$$\min_{w,b} \frac{1}{2} ||w||^2, s.t. y_i(w^Tx_i+b)>=1$$可以用现成的优化计算包求解(凸二次规划问题),但可以用更高效的拉格朗日乘子法,这样就得到其“对偶问题”。该问题的拉格朗日函数可写为
$$L(w,b,a) = \frac{1}{2} ||w||^2 + \sum_{i=1}^m \alpha_i (1-y_i(w^Tx_i+b))$$
而令$$L(w,b,a)$$对w和b的偏导为零可以得到对偶问题
$$\max_{\alpha} \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j x_i^Tx_j, s.t. \sum_{i=1}^{m}a_i y_i = 0, \alpha \ge 0$$
求解出$$\alpha$$(使用Sequential Minimal Optimization, SMO等算法)后可以得到模型
$$f(x) = \sum_{i=1}^{m}a_i y_i x_i^Tx + b$$
因为是不等式约束,因此上述过程需满足KKT(Karush-Kuhn-Tucker)条件,即
$$\left{\begin{matrix} \alpha \ge 0; \ y_i f(x_i) - 1 \ge 0; \ \alpha_i (y_i f(x_i)-1) =0. \end{matrix}\right.$$
由此可以得到支持向量机的一个重要性质:训练完成后,大部分的训练样本都不需保留,最终模型仅与支持向量有关。
核函数
前面假设训练样本集是线性可分的,然而实际任务中通常都不是线性可分的。对这样的问题,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。如果原始空间是有限维,即属性数有限,那么一定存在一个高维特征空间使样本可分。
令$$\phi(x)$$表示将x映射后的特征向量,则划分超平面可以定义为 $$f(x) = w^T \phi(x) + b$$。
定义核函数 $$\kappa(x) = \phi(x_i)^T\phi(x_j)$$,则可以得到
$$\max_{\alpha} \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y_i y_j \kappa(x_i, x_j), s.t. \sum_{i=1}^{m}a_i y_i = 0, \alpha \ge 0$$
求解后可得
$$f(x) = \sum_{i=1}^{m}a_i y_i \kappa(x, x_i) + b$$
常用核函数

此外核函数可通过函数组合得到,如线性组合、直积等组合方法。
软间隔
软间隔允许支持向量机在一些样本上出错,可以缓解核函数难以确定的问题。此时,优化目标为
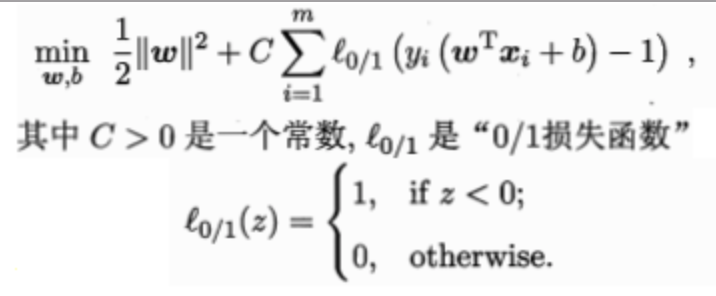
由于$$l_{0/1}$$函数数学性质不好(非凸、非连续),通常使用其他替代损失函数
- hinge损失:$$max(0, 1-z)$$
- 指数损失:$$exp(-z)$$
- 对率损失:$$log(1+exp(-z))$$
注意:若使用对率损失函数来替代0/1损失函数,则几乎得到了对率回归模型。实际上,支持向量机与对率回归的优化目标相近,性能也相当。对率回归的优势主要在于其输出具有自然的概率意义,即在给出预测标记的同时也给出了概率。
核方法
若不考虑偏移项,则无论SVM还是SVR,学得的模型总能表示成核函数的线性组合,且对损失函数没有限制,对正则化项仅要求单调递增,甚至不要求是凸函数。这意味着对于一般的损失函数和正则化项,优化问题的最优解都可表示为核函数的线性组合。这显示出核函数的巨大威力。
核方法就是对一系列基于核函数的学习方法的统称。最常见的就是通过“核化”(即引入核函数)来将线性学习器扩展为非线性学习器,如核线性判别分析(KLDA)等。