卷积神经网络
卷积神经网络(Convolutional Neural Network, CNN)是一种前馈神经网络,它的人工神经元可以响应一部分覆盖范围内的周围单元,对于大型图像处理有出色表现。卷积神经网络由一个或多个卷积层和顶端的全连通层(对应经典的神经网络)组成,同时也包括关联权重和池化层(pooling layer)。这一结构使得卷积神经网络能够利用输入数据的二维结构。与其他深度学习结构相比,卷积神经网络在图像和语音识别方面能够给出更优的结果。相比较其他深度、前馈神经网络,卷积神经网络需要估计的参数更少,使之成为一种颇具吸引力的深度学习结构。
卷积神经网络的核心思想
- 局部感受野:普通的多层感知器中,隐层节点会全连接到一个图像的每个像素点上;而在卷积神经网络中,每个隐层节点只连接到图像某个足够小局部的像素点上,从而大大减少需要训练的权值参数。比如1000×1000的图像,使用10×10的感受野,那么每个神经元只需要100个权值参数;不过由于需要将输入图像扫描一遍,共需要991×991个神经元(参数数目减少了一个数量级,不过还是太多)。
- 权值共享:在卷积神经网中,同一个卷积核内,所有的神经元的权值是相同的,从而大大减少需要训练的参数。继续前面的例子,虽然需要991×991个神经元,但是它们的权值是共享的,所以只需要100个权值参数,以及1个偏置参数。作为补充,在CNN中的每个隐藏,一般会有多个卷积核。
- 池化:在卷积神经网络中,没有必要一定就要对原图像做处理,而是可以使用某种“压缩”方法,这就是池化,也就是每次将原图像卷积后,都通过一个下采样的过程,来减小图像的规模。以最大池化(Max Pooling)为例,1000×1000的图像经过10×10的卷积核卷积后,得到的是991×991的特征图,然后使用2×2的池化规模,即每4个点组成的小方块中,取最大的一个作为输出,最终得到的是496×496大小的特征图。
Multilayer Perceptron (MLP, 多层感知机)
感知机只能解决线形可分问题,但对非线形可分问题(比如简单的异或)就无能为力了。通过将多个感知器按照一定的结构和系数进行组合,就构成了多层感知机。多层感知机层与层之间是全连接的(全连接的意思就是:上一层的任何一个神经元与下一层的所有神经元都有连接)。多层感知机最底层是输入层,中间是隐藏层,最后是输出层。
多层感知器存在的问题:
- 权值多:它是一个全连接的网络,在输入比较大的时候,权值会特别多。比如一个有1000个节点的隐层,连接到一个1000×1000的图像上,那么就需要 10^9 个权值参数(外加1000个偏置参数)!这一方面限制了每层能够容纳的最大神经元数目,另一方面也限制了多层感知器的层数即深度。
- 梯度发散:一般情况下,我们需要把输入归一化,而每个神经元的输出在激活函数的作用下也是归一化的;另外,有效的参数其绝对值也一般是小于1的;这样,在BP过程中,多个小于1的数连乘,得到的会是更小的值。也就是说,在深度增加的情况下,从后传播到前边的残差会越来越小,甚至对更新权值起不到帮助,从而失去训练效果,使得前边层的参数趋于随机化。
CNN结构
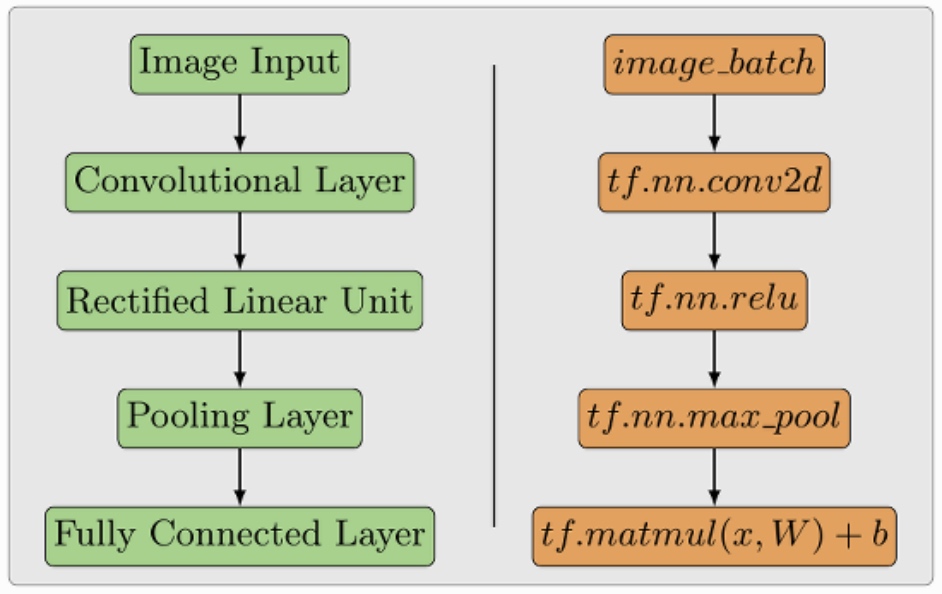
- 卷积层:对输入的图像进行特征提取。
- 激活函数层:积后的结果压缩到某一个固定的范围,这样可以一直保持一层一层下去的数值范围是可控的。
- 降采样层:对特征进行采样,即用一个数值替代一块区域,主要是为了降低网络训练参数及模型的过拟合程度。
- 标准化层:数据归一化。
- 全连接层:全连接层的每一个结点都与上一层的所有结点相连,用来把前边提取到的特征综合起来。由于其全相连的特性,一般全连接层的参数也是最多的。主要是为了分类或回归,当然也可以没有。
- Dropout层:在模型训练时随机让网络某些隐含层节点的权重不工作,不工作的那些节点可以暂时认为不是网络结构的一部分,但是它的权重得保留下来(只是暂时不更新而已),因为下次样本输入时它可能又得工作了。主要是为了防止过拟合。
每个层次的详细说明见这里.
Convolution (卷积,局部感受野)
对于离散函数$$f(x,y), g(x,y)$$的卷积一般定义为
$$f(m, n)*g(m, n) = \sum_u^\infty \sum_v^\infty {f(u, v)g(m - u, n - v)}$$
对应的,图像的卷积定义为
$$f(x) = act(\sum_{i, j}^n \theta_{(n - i)(n - j)} x_{ij} + b)$$
其计算过程为
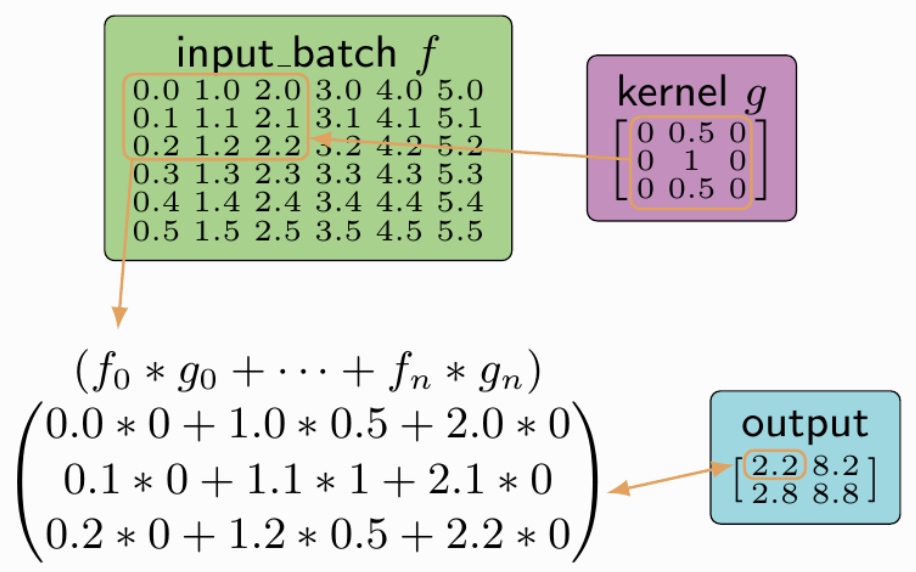
卷积的动态展示:
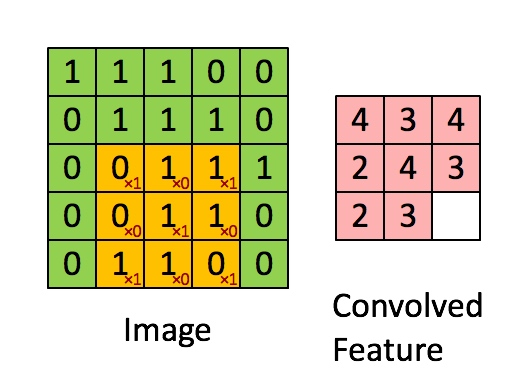
由于特征图的变长不一定是2的倍数,所以在边缘处理上也要注意:
- 忽略边缘(padding=‘VALID’):将多出来的边缘直接省去。
- 保留边缘(padding=‘SAME’):将特征图的变长用0填充为2的倍数,然后再池化(一般使用这种方式)。
import tensorflow as tf
input_batch = tf.constant([
[ # First Input
[[0.0], [1.0]],
[[2.0], [3.0]]
],
[ # Second Input
[[2.0], [4.0]],
[[6.0], [8.0]]
]
])
kernel = tf.constant([
[
[[1.0, 2.0]]
]
])
# strides parameter highlights how a convolution operation
# is working with a kernel.
# The data format has to be [batch_size, height, width, channel]
conv2d = tf.nn.conv2d(input_batch,
kernel,
strides=[1, 1, 1, 1],
padding='SAME')
with tf.Session() as sess:
print sess.run(conv2d)
# output ==>
# [[[[ 0. 0.]
# [ 1. 2.]]
#
# [[ 2. 4.]
# [ 3. 6.]]]
#
#
# [[[ 2. 4.]
# [ 4. 8.]]
#
# [[ 6. 12.]
# [ 8. 16.]]]]
input_batch = tf.constant([
[ # First Input (6x6x1)
[[0.0], [1.0], [2.0], [3.0], [4.0], [5.0]],
[[0.1], [1.1], [2.1], [3.1], [4.1], [5.1]],
[[0.2], [1.2], [2.2], [3.2], [4.2], [5.2]],
[[0.3], [1.3], [2.3], [3.3], [4.3], [5.3]],
[[0.4], [1.4], [2.4], [3.4], [4.4], [5.4]],
[[0.5], [1.5], [2.5], [3.5], [4.5], [5.5]],
],
])
kernel = tf.constant([ # Kernel (3x3x1)
[[[0.0]], [[0.5]], [[0.0]]],
[[[0.0]], [[1.0]], [[0.0]]],
[[[0.0]], [[0.5]], [[0.0]]]
])
# NOTE: the change in the size of the strides parameter.
conv2d = tf.nn.conv2d(input_batch,
kernel,
strides=[1, 3, 3, 1],
padding='SAME')
with tf.Session() as sess:
print sess.run(conv2d)
# output ==>
# [[[[ 2.20000005]
# [ 8.19999981]]
# [[ 2.79999995]
# [ 8.80000019]]]]
Pooling(池化, 下采样)
通过卷积层获得了图像的特征之后,理论上我们可以直接使用这些特征训练分类器(如softmax),但是这样做将面临巨大的计算量的挑战,而且容易产生过拟合的现象。为了进一步降低网络训练参数及模型的过拟合程度,对卷积层进行池化/采样(Pooling)处理。池化/采样的方式通常有以下两种:
- 最大池化(Max Pooling: 选择Pooling窗口中的最大值作为采样值;
- 均值池化(Mean Pooling): 将Pooling窗口中的所有值相加取平均,以平均值作为采样值
- 高斯池化:借鉴高斯模糊的方法。不常用。
- 可训练池化:使用一个训练函数$y=f(x)$。不常用。
图像经过池化后,得到的是一系列的特征图,而多层感知器接受的输入是一个向量。因此需要将这些特征图中的像素依次取出,排列成一个向量(这个过程被称为光栅化)。
CNN Summary
