Navigation :

决策树

决策树是一种常见的机器学习方法，它基于二元划分策略（类似于二叉树），如下图所示

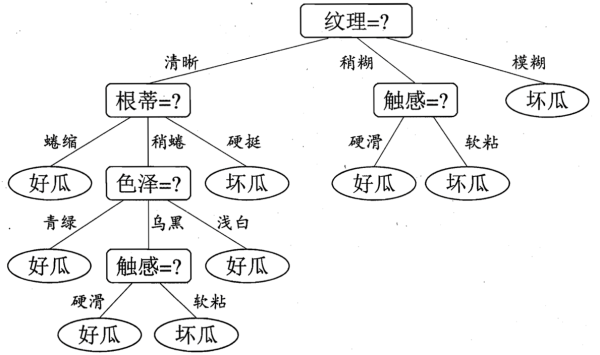
一棵决策树包括一个根节点、若干个内部节点和若干个叶节点。叶节点对应决策的结果，而其他节点对应一个属性测试。决策树学习的目的就是构建一棵泛化能力强的决策树。决策树算法的优点包括

使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。

决策树所形成的分类边界有一个明显特点：轴平行，即它的分类边界由多个与坐标轴平行的分段组成。在多变量决策树中，通过替换该分段为斜划分实现决策树模型的简化。

划分选择

决策树学习的关键是如何选择最优划分属性。一般来说，我们希望划分后分支节点所包含的样本尽量属于同一个类别，即节点的纯度（purity）越来越高。

信息熵是度量样本纯度的一种常用指标，$$End(D)$$ 越小则纯度越高。

$$Ent(D)=-\sum^y_{k=1}p_klog_2p_k$$

其中，$$p_k$$是第k类样本所占的比例，k=1,2,…,y。

而在属性选择时，要选择信息增益大的属性。其中，信息增益为

$$Gain(D, a) = Ent(D) - \sum^V_{v=1} \frac{|D^v|}{D} Ent(D^v)$$

ID3算法：以信息增益为准选择决策树的属性，注意信息增益偏好可取值数目较多的属性。
C4.5算法：使用增益率选择最优划分属性，增益率定义为 $$Gain_ratio(D, a) = \frac{Gain(D,a)}{IV(a)}$$，而 $$IV(a) = - \sum^V_{v=1}\frac{|D^v|}{D} log_2\frac{|D^v|}{D}$$。注意增益率偏好可取值数目较少的属性。
基尼指数：这是CART决策树使用的划分算法，$$Gini_{index}= \sum^V_{v=1} \frac{|D^v|}{D} Gini(D^v)$$ ，而 $$Gini(D)=-\sum^y_{k=1} \sum_{k’!=k} p_kp_{k’} = 1- \sum^y_{k=1} p_k^2$$。

剪枝（pruning）是决策树学习中解决过拟合问题的主要手段，其策略包括预剪枝和后剪枝两种。

预剪枝：在构造决策树的同时进行剪枝，对每个节点进行划分前的估计，如果不能带来决策树泛化性能的提升则停止划分并将当前节点标记为叶节点。预剪枝有带来欠拟合的风险。
后剪枝：决策树构造完成后进行剪枝，自底向上对非叶节点考察，如果该节点的子树替换为子树的叶节点可以提升泛化性能，则替换该子树为其叶节点。后剪纸的欠拟合风险很小，泛化性能通常优于预剪枝，但计算量大，训练时间较长。