梯度下降
在训练机器学习模型时,首先对权重和偏差进行初始猜测,然后反复调整这些猜测,直到获得损失可能最低的权重和偏差为止(即模型收敛)。
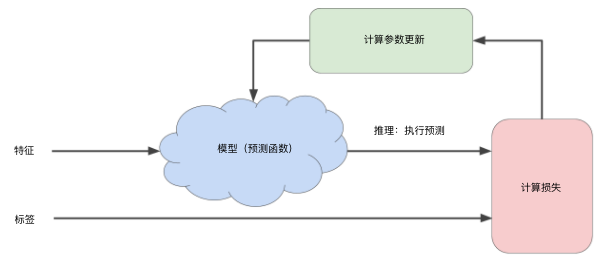
而梯度下降是机器学习中最常用的计算代价函数的方法,它只需要计算损失函数的一阶导数。
假设 h(theta) 为目标函数,而 J(theta) 为损失函数,
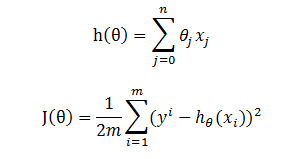
损失函数的梯度(即偏导数)为
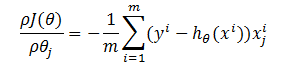
按参数 theta 的梯度负方向,来更新 theta,即梯度下降算法为
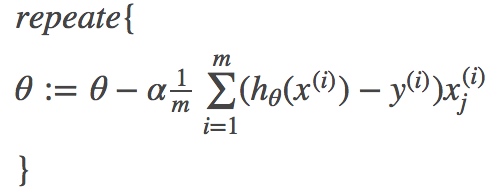
mini-batch 梯度下降
前面的梯度下降算法在每一轮迭代均需要所有样本参与,对于大规模的机器学习应用,计算复杂度非常高。因此在每次迭代只利用部分训练集样本,即 mini-batch 梯度下降算法。实践表明,在小批量或甚至包含一个样本的批量上执行梯度下降法通常比全批量更高效。
假设训练集有 m 个样本,每个 mini-batch(训练集的一个子集)有 b 个样本,那么,整个训练集可以分成 m/b 个 mini-batch。我们用 ω 表示一个 mini-batch, 用 Ωj 表示第 j 轮迭代中所有 mini-batch 集合,有:
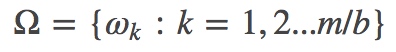
那么,mini-batch 算法为
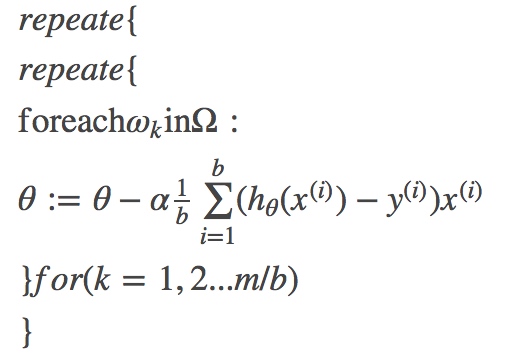
随机梯度下降
随机梯度下降(SGD)通过每个样本来迭代更新一次 $\theta$, 它大大加快了迭代速度。
随机梯度下降算法是 mini-batch 的一个特殊应用。SGD 等价于 b=1 的 mini-batch 梯度下降算法。即每个 mini-batch 中只有一个训练样本。