激活函数
激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
Sigmoid
也成为 S 形函数,取值范围为 (0,1)。Sigmoid 将一个实数映射到 (0,1) 的区间,可以用来做二分类。Sigmoid 在特征相差比较复杂或是相差不是特别大时效果比较好。
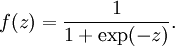
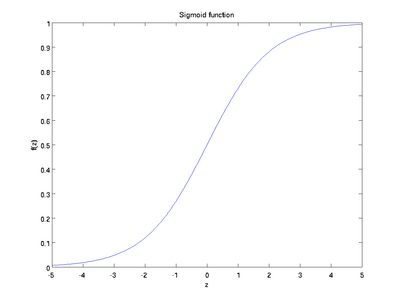
sigmoid 缺点:
- 激活函数计算量大(指数运算),反向传播求误差梯度时,求导涉及除法
- 对于深层网络,sigmoid 函数反向传播时,很容易就会出现梯度消失的情况(在 sigmoid 接近饱和区时,变换太缓慢,导数趋于 0,这种情况会造成信息丢失),从而无法完成深层网络的训练
Tanh
也称为双切正切函数,取值范围为 [-1,1]。tanh 在特征相差明显时的效果会很好,在循环过程中会不断扩大特征效果。
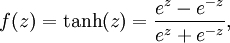
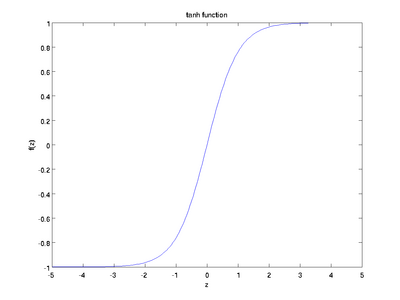
Softmax
softmax 函数将 K 维的实数向量压缩(映射)成另一个 K 维的实数向量,其中向量中的每个元素取值都介于 (0,1) 之间。常用于多分类问题。
Softmax is a generalization of the logistic function that “squashes” a K-dimensional vector
zof arbitrary real values to a K-dimensional vectorsigma(z)of real values in the range(0, 1)that add up to 1.
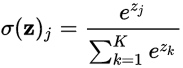
ReLU
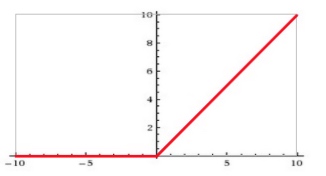
为什么采用 ReLU:
- sigmoid 等激活函数(指数运算)计算量大,并且在深层网络上容易出现梯度消失问题
- ReLU 计算量小(不涉及除法),一部分神经元的输出为 0 造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生
对于偏置值,如果用 ReLU 的话,最好的办法就是把它们都初始化成小的正值,这样神经元一开始就会工作在 ReLU 的非零区域内。
ReLU 缺点:强制的稀疏处理会减少模型的有效容量(即特征屏蔽太多,导致模型无法学习到有效特征)。